Euclidean distance ในทางคณิตศาสตร์ Euclidean distance หรือ Euclidean metric คือ ระยะทาง ระหว่าง2จุด จุดที่จะวัดนั้นมีเงื่อนไขมีหลายค่าจากหลายมิติหรือขนาดขึ้นกับรูปแบบ ซึ่งสามารถพิสูจน์หาค่าได้ด้วยทฤษฎีของ Pythagorean เมื่อมีการใช้สูตรเพื่อหาระยะทาง ขนาดของ Euclidean จะเป็นเซตของ Vector
นิยาม
Euclidean ระยะทางระหว่างจุด 
และ 
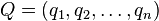ใน Euclidean หลายขนาด,ระบุได้เป็น:
ระยะทางในขนาด1มิติ
หาระยะทางระหว่าง2จุดในขนาด1มิติ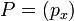 
และ 
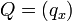, หาระยะทางได้โดย:
ระยะทางในขนาด2มิติ
หาระยะทางระหว่าง2จุดในขนาด2มิติ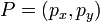 
และ 
, หาระยะทางได้โดย:
ดัดแปลง, แสดงในรูป polar coordinates, ใช้ 
และ 
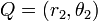, หาระยะทางได้โดย:
ระยะทางในขนาด3มิติ
หาระยะทางระหว่าง2จุดในขนาด3มิติ 
และ 
, หาระยะทางได้โดย:
ระยะทางในขนาดหลายมิติ
หาระยะทางระหว่าง2จุดในขนาดหลายมิติ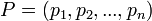 
และ 
, หาระยะทางได้โดย:
Credit: http://en.wikipedia.org/wiki/Euclidean_distance
