บทความนี้ได้นำส่วน QoS Matchmaking Process มาเขียนโดยสรุปโดยไม่ได้ลงลึกในรายละเอียด มาจากงานวิจัยเรื่อง
A Framework and QoS Matchmaking Algorithm for Dynamic Web Services Selection เป็นงานวิจัยของ
L.Taher
Department of Computer Science, University of Sharjah, Sharjah, P.O.Box 27272,UAE
H. El Khatib
College of Information Technology, UAE University,Al Ain, P.O.Box 17555,UAE
R.Basha
Department of Computer Science, University of Sharjah, Sharjah, P.O.Box 27272, UAE
Correspondence Email: ltaher@eim.ae
งานวิจัยนี้เป็นการสร้างเฟรมเวิร์คเพื่อให้บริการค้นหา เว็บเซอร์วิสด้วย คุณภาพของเซอร์วิส โดยเน็นที่การค้นหาเซอร์วิสที่มีคุณภาพของเซอร์วิสที่ใกล้เคียงกับเซอร์วิส ที่มีคุณภาพของเซอร์วิสตามความต้องการของผู้สืบค้น เนื่องจากผู้เขียนมีความสนใจที่จะทำการปรับปรุงขั้นตอนวิธีในค้นหาเซอร์วิส ของงานวิจัยนี้จึงได้นำเฉพาะ ส่วนขั้นตอนวิธีในการค้นหามาสรุปและนำเสนอในบทความนี้
บทความนี้เขียนโดยสรุปตามความเข้าใจของผู้เขียนเอง หากผิดพลาดประการณ์ใดต้องขออภัยผู้ที่สละเวลามาอ่านด้วย
QoS Matchmaking Process
เป็นกรรมวิธีที่จะได้มาซึ่งเซอร์วิสที่มีคุณภาพของเซอร์วิสตรงตามความต้องการของผู้สืบค้น โดยในงานวิจัยนี้จะเป็นการหา ระยะห่างระหว่างคุณภาพของเซอร์วิสที่ ผู้สืบค้นต้องการ กับเซอร์วิสที่มีข้อมูลคุณภาพของเซอร์วิสที่ทางผู้ให้บริการสืบค้นมีอยู่ในฐานข้อมูล ที่มีฟังก์ช้นการทำงานตรงกับที่ผู้สืบค้นต้องการ โดยใช้หลักการของ Euclidean distance ซึ่งเคยเขียนอธิบายไปแล้วเข้ามาใช้ในขั้นตอนวิธี QoS Matchmaking ของงานวิจัยนี้
Euclidean distanceเป็นวิธีที่จะใช้ในการวัดระยะห่างระหว่าง Vector สอง Vector คุณภาพของเซอร์วิสจะถูกมองเป็นสมาชิกภายใน Vector เนื่อง จากคุณภาพของเซอร์วิสนั้นจะประกอบไปด้วยคุณสมบัติหลายๆ อย่างที่แต่ละงานวิจัยได้นำมาใช้เพื่อหาความใกล้เคียงกันในคุณภาพของ เซอร์วิส เซอร์วิสที่ผู้สืบค้นจะพบ คือเซอร์วิสที่อยู่ในฐานข้อมูลของผู้ให้บริการที่ มีค่า Euclidean distance น้อยที่สุดเมื่อเปรียบเทียบคุณภาพของเซอร์วิส กับคุณภาพของเซอร์วิสที่ผู้สืบค้นต้องการ
Quality of Web Service Dataset example in JSP : Sample search ใน Algorithm 1 ของ web page นี้ผู้เขียนได้ใช้ QoS Matchmaking Algorithm จากงานวิจัยนี้ สร้างขึ้นมา ผลลัพธ์ที่เห็นเป็นตารางด้านล่างนั้น จะแสดง service ทั้งหมดใน DOMAIN ที่ตรงกับ Keyword ที่ใส่เข้ามา เรียงลำดับตามเซอร์วิสที่มีคุณภาพดี่ที่สุด(จากงานวิจัยอื่นเนื่องจากผู้เขียนได้นำฐานข้อมูลของงานวิจับอื่นมาประยุกต์ใช้) เซอร์วิสที่เป็นคำตอบคือเซอร์วิสที่มีค่า Euclidean distance น้อยที่สุด ต้องขออภัยที่ไม่ได้ทำให้เห็นชัดเจนต้องสังเกตุเองจากในตาราง จะเห็นได้ว่าเซอร์วิสที่มีคุรภาพของเซอร์วิสที่ผู้สืบค้นต้องการจะไม่ใช้เซอร์วิสที่ดีที่สุดเสมอไป ส่วน Alogrithm 2 - My Algorithm ผู้เขียนจะพยายามทำต่อไป
ทีแรกก็จะเขียนแบบลงรายละเอียดแต่การพิมพ์ equation แล้วเก็บเป็นภาพอัพขึ้นบลอคมันยุ่งยากมากมาย จึงเขียนโดยสรุปๆ แบบลงรายละเอียดคงจะเขียนไว้ในบลอคปิดเท่านั้น

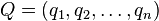

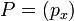
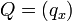 ,
, 
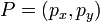
 ,
,

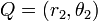 ,
, 

 ,
,
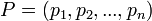
 ,
, 